Tema 6: Potenciación, Radicación y Racionalización
6.2.1. Leyes de los radicales
La potenciación y la radicación son unos de los métodos más usados en el lenguaje matemático para ordenar, medir, y calcular. Gracias a la existencia de estas operaciones y sus propiedades, el ser humano ha podido calcular y expresar figuras, cuerpos, volúmenes, áreas, códigos y sistemas que organizan y mejoran nuestra calidad de vida. Explora las propiedades indispensables para comprender y expresar el lenguaje matemático en la radicación:
Haz clic en cada tema para ampliar la información
Regla 1
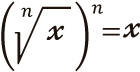
Si el índice de una raíz es igual al exponente del todo, se cancela el índice con el exponente del todo, obteniendo como resultado el radicando. Veamos:
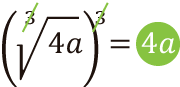
Regla 2
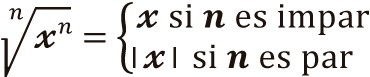
Si es impar
Si en una expresión el exponente y el índice son impares, el resultado de la operación es igual al radicando.
Ejemplo:

Si es par
Si en una expresión el exponente y el índice son pares, el resultado de la operación es igual al valor absoluto del radicando.
Ejemplo:

Regla 3

Cuando se tiene la raíz de una multiplicación, esto será igual a la multiplicación de las raíces, es decir, resolvemos de manera independiente cada raíz y luego se multiplican los resultados para obtener la raíz de la expresión inicial. Veamos:
Ejemplo:
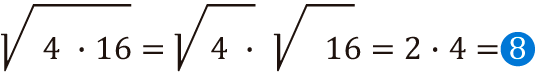
Por lo tanto:
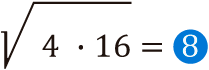
Regla 4
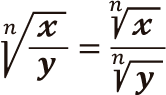
Cuando se tiene una raíz de una división o fraccionario, su resultado es igual a la raíz del numerador sobre la raíz del denominador. Veamos:
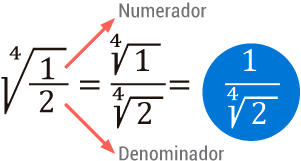
Por tanto:
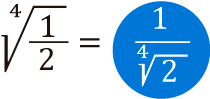
Regla 5
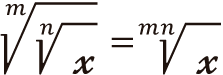
Si se tiene una raíz con un índice m y dentro de esa raíz hay otra con índice n de la base X, esto será igual a la raíz de índice m . n de la base X, es decir, se multiplican los índices, conservando el mismo radicando.
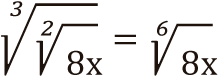
Veamos otro ejemplo, aplicando simultáneamente lo aprendido hasta ahora:
