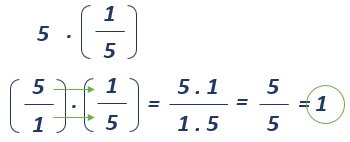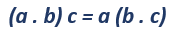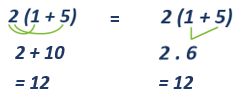La propiedad clausurativa

La suma y el producto de dos números reales da como resultado otro número real. Lo que podemos expresar de la siguiente manera:

Esto significa que la suma y el producto son operaciones cerradas

Ejemplos:

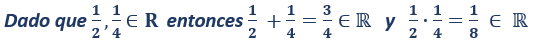
La propiedad conmutativa

El orden en que se sumen o multipliquen dos o más números reales no altera el resultado

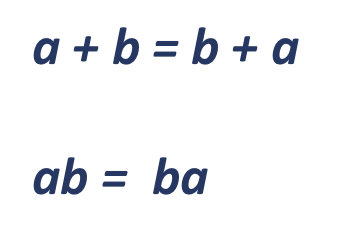
Representamos un ejemplo de la expresión:

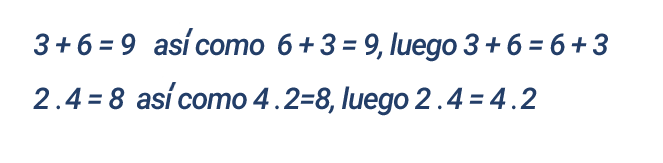
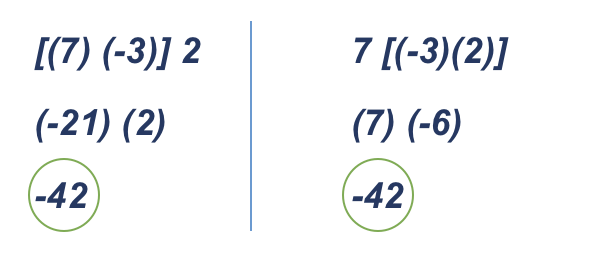
La propiedad asociativa

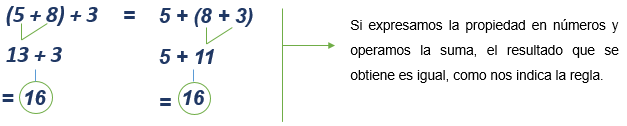
El resultado de la suma o el producto de tres o más números es independiente de la forma en que se agrupen los números. Para expresar esta propiedad, se escribe:

Aplicación en la multiplicación

La propiedad distributiva

Es una propiedad que comparten las operaciones multiplicación y suma. Se aplica siempre que tengamos un número multiplicando a la suma de dos o más números dentro de paréntesis. De manera que el número que esté por fuera del paréntesis se multiplica por cada uno de los términos o sumandos que hay en la operación. Veamos:

Nombremos los elementos para entender la propiedad:

Aplicación

Elemento neutro para la suma

El elemento neutro para la suma es el 0 ya que cualquier número sumado con cero dará como resultado el mismo número.

Si expresamos en números esta propiedad, se escribe así:

Elemento neutro para el producto (multiplicación)

El elemento neutro para la multiplicación es 1, es decir, cualquier número multiplicado por 1, da como resultado el mismo número.

Si trasladamos esta propiedad a una operación con números, podremos recordar lo que aprendimos desde la escuela con la tabla del 1:

Inverso aditivo

Sean 𝑎 y 𝑏 números Reales, si al sumar 𝑎 a un número 𝑏 el resultado es cero, se le puede llamar a este numero 𝑏 como el inverso aditivo de 𝑎 y la magnitud de 𝑏=−𝑎. La notación para esta propiedad se expresa de la siguiente manera:

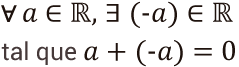
En este caso, podemos ilustrar un ejemplo reemplazando a por un número positivo y sumándolo con su número inverso, o sea negativo, para realizar la operación:

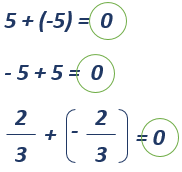
Inverso multiplicativo o recíproco

Esta propiedad también conocida como cociente unidad, se refiere al valor inverso de una unidad. Si se tiene el elemento a su inverso multiplicativo es 1/a o a^-1 lo cual se denota de la siguiente manera:

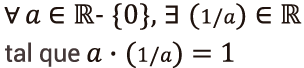
Ahora observemos el inverso multiplicativo del número 5:

Entonces obtenemos el mismo resultado si el 5 entero lo convertimos en una fracción 5/1 y aplicamos la operación de multiplicación de fraccionarios, hasta simplificar la fracción.