Tema 3: Valor Absoluto y Distancia
3.2. Definición de valor absoluto o módulo de un número
Se define como valor absoluto de
Sea
Dado que la distancia entre dos números siempre es positiva, entonces
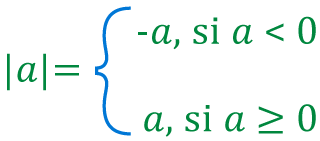
Recta valor absoluto
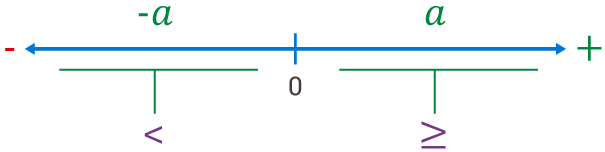

Analiza la notación de la expresión dada e interpreta la aplicación de valor absoluto:
|3-5| = |-2| = - (-2) = 2 ya que 3 < 5
|e - π | = - (e - π ) ya que e < π
Aplicación valor absoluto
Para interpretar lo anterior:
|3-5| =
Simplifiquemos
|3-5| = |-2|
Apliquemos la definición
|-2| = -(-2)
Determinemos el valor absoluto
de la expresión resultante
-(-2) = 2
Si entendemos la definición del valor absoluto y su lógica, podemos trasladar su aplicación en acciones cotidianas de nuestra vida. Un ejemplo simple son las distancias que recorremos a diario, la medición de la altitud, el desplazamiento del ascensor, entre otros:
Si estás de pie en un lugar y decides caminar X cantidad de metros, dices “caminé 20 metros”, pero si decides retroceder no vas a decir "caminé -20 metros", pues independientemente del sentido, la distancia continúa siendo absoluta.